How To Use Simple Shape Drawing

Alice Hubbard, Providence, United States, ca. 1892. Photo: Zindman/Freemont.

Shapes

Finally! We have been building skills for this moment! You have learned most of the GLSL foundations, types and functions. Yous have practiced your shaping equations over and over. Now is the time to put it all together. You lot are up for this challenge! In this chapter yous'll learn how to draw uncomplicated shapes in a parallel procedural manner.

Rectangle

Imagine we accept grid paper similar we used in math classes and our homework is to draw a square. The newspaper size is 10x10 and the square is supposed to be 8x8. What will you do?

You'd paint everything except the showtime and last rows and the first and last column, right?

How does this relate to shaders? Each little square of our grid paper is a thread (a pixel). Each little foursquare knows its position, like the coordinates of a chess board. In previous chapters we mapped x and y to the red and green color channels, and we learned how to utilise the narrow two dimensional territory between 0.0 and one.0. How can nosotros apply this to describe a centered square in the middle of our billboard?

Allow'southward start by sketching pseudocode that uses if statements over the spatial field. The principles to practice this are remarkably similar to how we recollect of the grid newspaper scenario.

          if ( (X GREATER THAN 1) AND (Y GREATER THAN one) )     paint white else     pigment black

Now that we have a meliorate idea of how this volition work, permit'south replace the if statement with stride(), and instead of using 10x10 allow'south use normalized values between 0.0 and one.0:

          compatible vec2 u_resolution;  void principal(){     vec2 st = gl_FragCoord.xy/u_resolution.xy;     vec3 colour = vec3(0.0);      // Each result will render ane.0 (white) or 0.0 (black).     float left = step(0.1,st.x);   // Similar to ( 10 greater than 0.1 )     bladder bottom = footstep(0.i,st.y); // Similar to ( Y greater than 0.i )      // The multiplication of left*bottom will be similar to the logical AND.     color = vec3( left * bottom );      gl_FragColor = vec4(color,1.0); }

The step() function will turn every pixel below 0.1 to black (vec3(0.0)) and the rest to white (vec3(i.0)) . The multiplication between left and bottom works as a logical AND operation, where both must be 1.0 to return ane.0 . This draws 2 black lines, one on the bottom and the other on the left side of the canvas.

In the previous code we repeat the structure for each axis (left and bottom). Nosotros can salvage some lines of code past passing two values direct to step() instead of ane. That looks like this:

          vec2 borders = pace(vec2(0.one),st); float pct = borders.x * borders.y;

And then far, nosotros've only drawn two borders (bottom-left) of our rectangle. Let'due south do the other two (elevation-right). Check out the post-obit code:

Uncomment lines 21-22 and see how we capsize the st coordinates and repeat the aforementioned step() function. That manner the vec2(0.0,0.0) will exist in the top right corner. This is the digital equivalent of flipping the page and repeating the previous procedure.

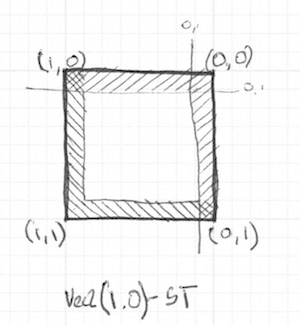
Take notation that in lines 18 and 22 all of the sides are existence multiplied together. This is equivalent to writing:

          vec2 bl = pace(vec2(0.1),st);       // bottom-left vec2 tr = step(vec2(0.1),1.0-st);   // top-correct color = vec3(bl.x * bl.y * tr.10 * tr.y);

Interesting right? This technique is all about using step() and multiplication for logical operations and flipping the coordinates.

Before going forward, attempt the following exercises:

Change the size and proportions of the rectangle.
Experiment with the same code but using smoothstep() instead of step(). Note that by changing values, you tin go from blurred edges to elegant shine borders.
Practice another implementation that uses floor().
Choose the implementation you like the nigh and make a function of it that y'all can reuse in the future. Make your role flexible and efficient.
Brand another function that just draws the outline of a rectangle.
How do you lot recollect you lot tin can move and identify different rectangles in the same billboard? If you effigy out how, show off your skills by making a composition of rectangles and colors that resembles a Piet Mondrian painting.

Piet Mondrian - Tableau (1921)

Circles

It's piece of cake to draw squares on filigree paper and rectangles on cartesian coordinates, but circles require some other approach, especially since nosotros demand a "per-pixel" algorithm. One solution is to re-map the spatial coordinates so that we tin can use a pace() part to draw a circumvolve.

How? Permit's start by going back to math class and the grid paper, where nosotros opened a compass to the radius of a circumvolve, pressed one of the compass points at the center of the circumvolve and then traced the edge of the circumvolve with a simple spin.

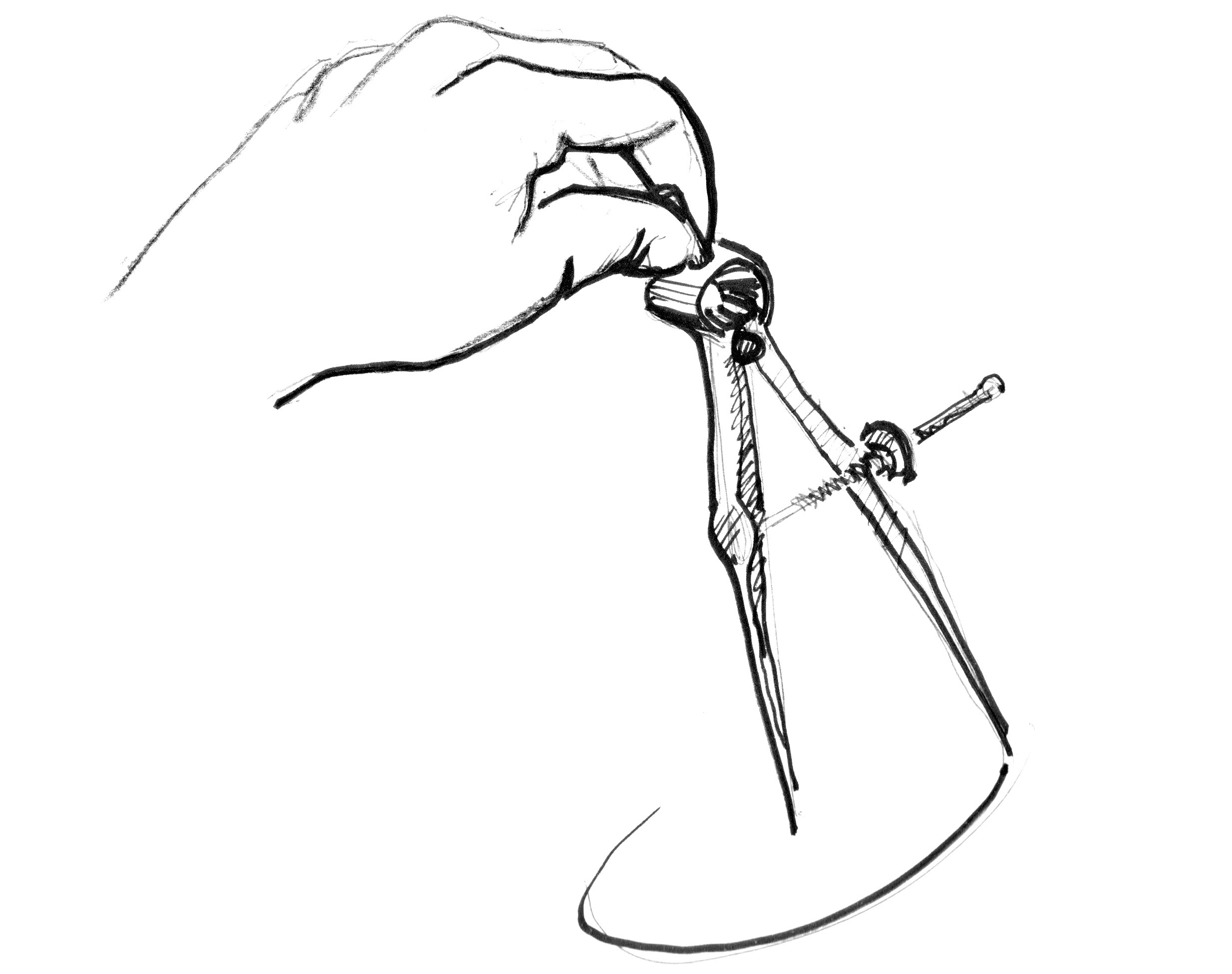
Translating this to a shader where each square on the grid paper is a pixel implies asking each pixel (or thread) if information technology is inside the area of the circumvolve. We do this by computing the altitude from the pixel to the center of the circle.

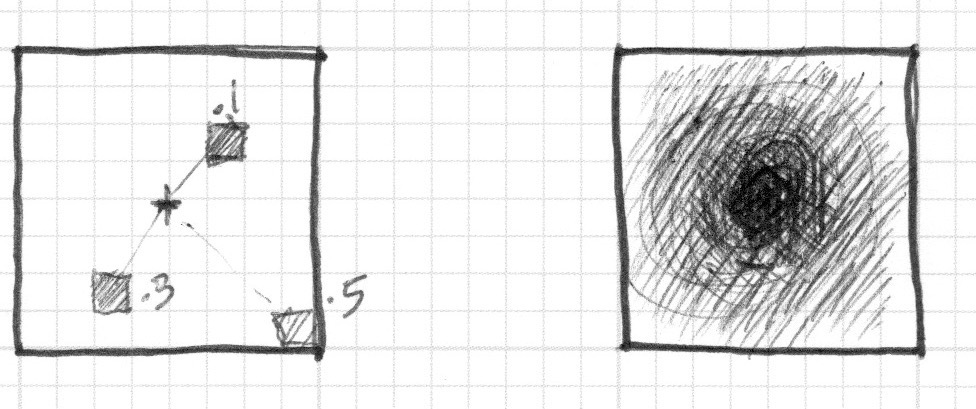
At that place are several ways to summate that altitude. The easiest one uses the distance() function, which internally computes the length() of the deviation betwixt two points (in our case the pixel coordinate and the eye of the canvas). The length() function is nothing only a shortcut of the hypotenuse equation that uses square root (sqrt()) internally.

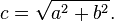
You tin can use distance(), length() or sqrt() to summate the distance to the heart of the billboard. The following code contains these 3 functions and the not-surprising fact that each i returns exactly same issue.

Comment and uncomment lines to endeavour the different ways to get the aforementioned result.

In the previous example we map the distance to the middle of the billboard to the color brightness of the pixel. The closer a pixel is to the centre, the lower (darker) value information technology has. Notice that the values don't get too high because from the middle ( vec2(0.5, 0.five) ) the maximum distance barely goes over 0.v. Contemplate this map and recall:

What you can infer from it?
How we can use this to draw a circle?
Modify the in a higher place code in order to contain the entire circular gradient inside the canvas.

Distance field

Nosotros can also call up of the higher up example equally an altitude map, where darker implies taller. The gradient shows us something like to the pattern made past a cone. Imagine yourself on the top of that cone. The horizontal distance to the edge of the cone is 0.5. This will be abiding in all directions. Past choosing where to "cutting" the cone you will get a bigger or smaller circular surface.

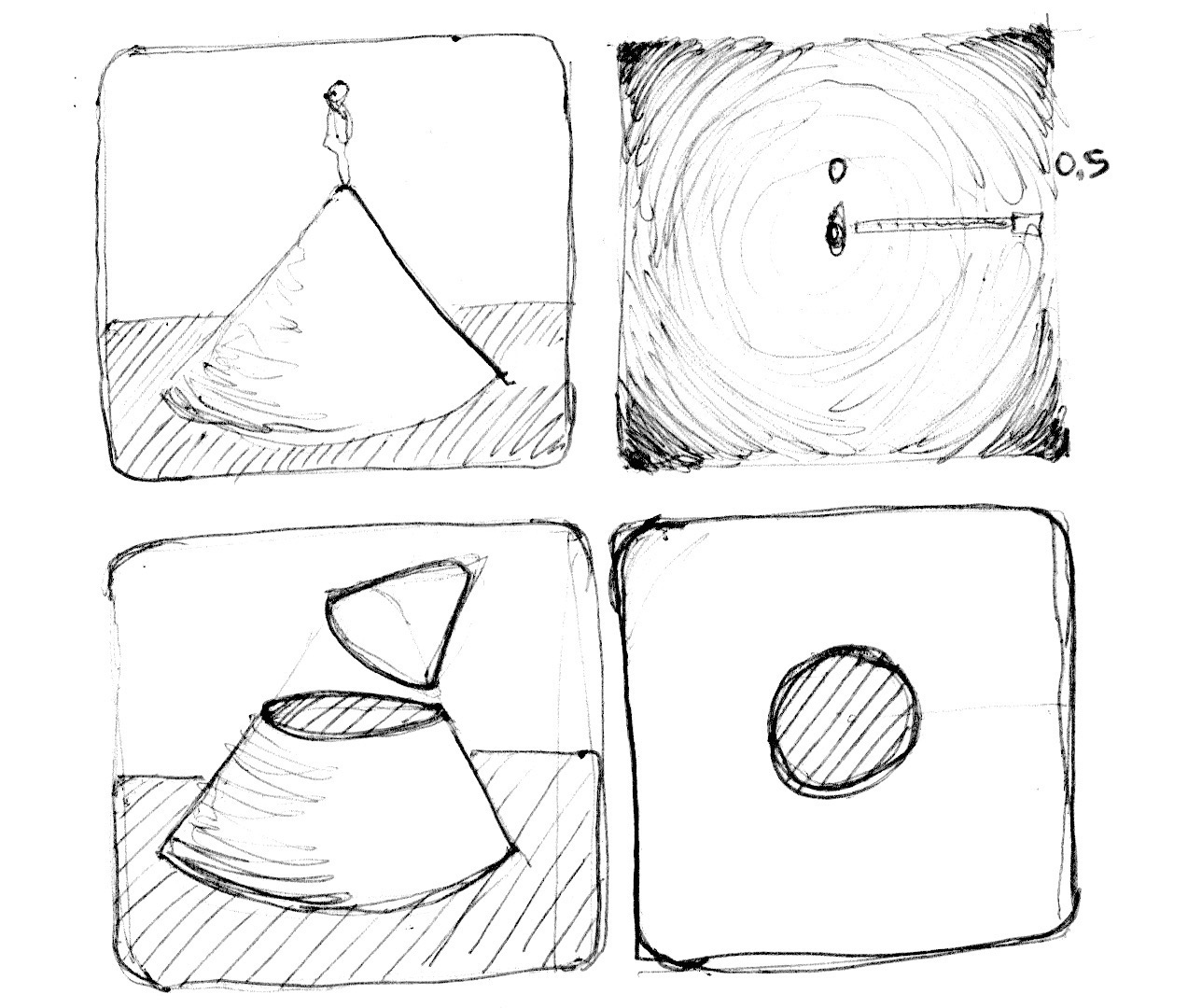
Basically we are using a re-estimation of the space (based on the distance to the center) to make shapes. This technique is known as a "distance field" and is used in different means from font outlines to 3D graphics.

Attempt the following exercises:

Use pace() to turn everything in a higher place 0.5 to white and everything below to 0.0.
Inverse the colors of the groundwork and foreground.
Using smoothstep(), experiment with unlike values to get dainty shine borders on your circumvolve.
Once you lot are happy with an implementation, make a function of it that y'all can reuse in the future.
Add color to the circle.
Tin can y'all breathing your circle to grow and shrink, simulating a beating heart? (You lot tin can become some inspiration from the animation in the previous chapter.)
What near moving this circle? Can you move it and identify different circles in a unmarried billboard?
What happens if y'all combine distances fields together using dissimilar functions and operations?

          pct = altitude(st,vec2(0.four)) + distance(st,vec2(0.6)); percentage = distance(st,vec2(0.4)) * distance(st,vec2(0.half dozen)); pct = min(distance(st,vec2(0.4)),altitude(st,vec2(0.6))); pct = max(altitude(st,vec2(0.iv)),distance(st,vec2(0.6))); pct = pw(distance(st,vec2(0.4)),distance(st,vec2(0.6)));

Make iii compositions using this technique. If they are animated, fifty-fifty amend!

For your tool box

In terms of computational power the sqrt() office - and all the functions that depend on it - tin be expensive. Here is another way to create a circular distance field past using dot() production.

Useful backdrop of a Altitude Field

Zen garden

Distance fields can be used to draw almost everything. Obviously the more complex a shape is, the more than complicated its equation will be, but once you lot accept the formula to make distance fields of a item shape it is very easy to combine and/or apply effects to it, similar polish edges and multiple outlines. Because of this, distance fields are popular in font rendering, like Mapbox GL Labels, Matt DesLauriers Material Design Fonts and as is described on Chapter 7 of iPhone 3D Programming, O'Reilly.

Take a look at the following lawmaking.

We starting time by moving the coordinate organisation to the heart and shrinking it in one-half in order to remap the position values betwixt -ane and ane. Also on line 24 nosotros are visualizing the altitude field values using a fract() function making it like shooting fish in a barrel to see the pattern they create. The distance field pattern repeats over and over similar rings in a Zen garden.

Let's take a look at the distance field formula on line 19. At that place we are calculating the altitude to the position on (.3,.three) or vec3(.3) in all four quadrants (that'due south what abs() is doing there).

If y'all uncomment line twenty, you will note that nosotros are combining the distances to these four points using the min() to zero. The result produces an interesting new pattern.

Now try uncommenting line 21; nosotros are doing the same but using the max() function. The issue is a rectangle with rounded corners. Note how the rings of the altitude field get smoother the further away they get from the heart.

Finish uncommenting lines 27 to 29 ane by 1 to understand the different uses of a distance field pattern.

Polar shapes

Robert Mangold - Untitled (2008)

In the chapter about color we map the cartesian coordinates to polar coordinates by calculating the radius and angles of each pixel with the post-obit formula:

          vec2 pos = vec2(0.v)-st; float r = length(pos)*2.0; bladder a = atan(pos.y,pos.x);

We utilise part of this formula at the showtime of the chapter to draw a circumvolve. Nosotros calculated the distance to the centre using length(). Now that we know about altitude fields we tin can learn another way of drawing shapes using polar coordinates.

This technique is a trivial restrictive but very simple. It consists of changing the radius of a circumvolve depending on the angle to achieve different shapes. How does the modulation work? Yes, using shaping functions!

Beneath you volition find the aforementioned functions in the cartesian graph and in a polar coordinates shader example (betwixt lines 21 and 25). Uncomment the functions ane-past-1, paying attention the relationship betwixt one coordinate system and the other.

Try to:

Breathing these shapes.
Combine dissimilar shaping functions to cut holes in the shape to make flowers, snowflakes and gears.
Utilize the plot() function we were using in the Shaping Functions Chapter to draw just the contour.

Combining powers

At present that we've learned how to modulate the radius of a circle co-ordinate to the angle using the atan() to draw different shapes, we tin learn how apply atan() with distance fields and use all the tricks and effects possible with distance fields.

The trick will use the number of edges of a polygon to construct the altitude field using polar coordinates. Bank check out the post-obit lawmaking from Andrew Baldwin.

Using this example, make a function that inputs the position and number of corners of a desired shape and returns a distance field value.
Mix distance fields together using min() and max().
Choose a geometric logo to replicate using distance fields.

Congratulations! You lot have made it through the rough function! Accept a break and let these concepts settle - drawing elementary shapes in Processing is easy but not here. In shader-state drawing shapes is twisted, and it can be exhausting to adapt to this new paradigm of coding.

Down at the end of this affiliate you lot will discover a link to PixelSpirit Deck this deck of cards will help y'all acquire new SDF functions, compose them into your designs and use on your shaders. The deck has a progressive learning curve, so taking ane card a day and working on it will push and claiming your skills for months.

Now that you know how to draw shapes I'm sure new ideas will pop into your mind. In the following chapter you will learn how to movement, rotate and scale shapes. This volition allow y'all to brand compositions!